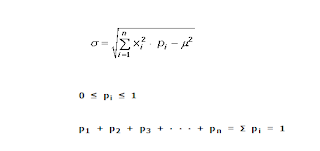Conjuntos
En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes:personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.
Ejemplo: el conjunto de los colores del arcoíris es:
- AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}
Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:
- P = {2, 3, 5, 7, 11, 13, ...}
Un conjunto queda definido únicamente por sus miembros y por nada más. En particular, un conjunto puede escribirse como una lista de elementos, pero cambiar el orden de dicha lista o añadir elementos repetidos no define un conjunto nuevo

Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos —los polígonos regulares en la imagen— es otro conjunto, en particular, un subconjunto del primero.
Unión
la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los elementos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los números impares positivos
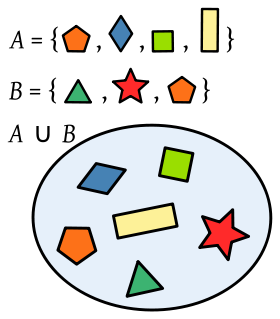
La unión de los conjuntos A y B es otro conjunto A ∪ B que contiene todos los elementos de A y de B.
Intersección
la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D :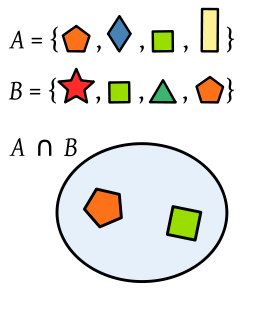
La intersección de A y B es otro conjunto A ∩ B que contiene sólo los elementos que pertenecen tanto a A como a B.
Diferencia
la diferencia entre dos conjuntos es una operación que resulta en otro conjunto, cuyos elementos son todos aquellos en el primero de los conjuntos iniciales que no estén en el segundo. Por ejemplo, la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I:

La diferencia entre los conjuntosA y B (y viceversa) es otro conjunto con todos los elementos del «minuendo», salvo los contenidos en el «sustraendo».
suceso complementario
Dado un suceso cualquiera A, se llama suceso complementario al formado por todos aquellos sucesos elementales que no están en A y se nota por Ac.
Si en el experimento "lanzar un dado" se define el suceso A = "salir un múltiplo de tres" A={3,6}, entonces Ac = {1,2,4,5}.
De la definición de suceso complementario se deduce inmediatamente que:
- A U Ac =
- A